| Projektname | Laufzeit |
|---|---|
| 2024 - 2027 | |
| 2023 - 2025 | |
| 2022 - 2026 | |
| Mehrskalen-Algorithmen und Simulation für die patientenspezifische Optimierung von endovaskulären Eingriffen bei zerebralen Aneurysmen | 2021 - 2027 |
| Mehrskalige Modellierung des thermomechanischen Reibkontakts von komplexen Problemen in technischen Anwendungen | 2021 - 2025 |
| 2021 - 2026 | |
| 2021 - 2024 | |
| Nutzung der Eigenfrequenzen zur Identifikation von Rissen | 2021 - jetzt |
| 2021 - 2025 | |
| Kombination von Daten- und Physik-basierten Methoden in hybriden digitalen Zwillinge | 2021 - 2026 |
Stabile Diskretisierungsverfahren und skalierbare Gleichungslöser für eingebettete Faser/Festkörper-Kopplung
| Fördergeber | Deutsche Forschungsgemeinschaft (DFG) |
| Laufzeit | 2024 - 2027 |
| Kurzbeschreibung |
Dieses Projekt zielt auf die Entwicklung robuster und stabiler Diskretisierungstechniken und effizienter iterativer Gleichunslöser für gemischt-dimensionale Finite-Elemente-Modelle von faserverstärkten Kontinua ab. Dabei werden eindimensionale (1D) Fasern mit Balkenmodellen dargestellt, die in einen dreidimensionalen (3D) homogenen Festkörper eingebettet sind, um eine hohe Modellierungsgenauigkeit zu erreichen. Die Innovation liegt in der Aufbringung der Kopplungsbedingungen über ein Lagrange-Multiplikator-Feld, um die schlechte Konditionierung der bisher verwendeten Penalty-Methoden zu überwinden. Aus einem tiefen Verständnis des Zusammenspiels zwischen Lösungsalgorithmen und numerischen Modellen werden schnelle und effiziente Lösungsverfahren resultieren, die für Computerarchitekturen der nächsten Generation geeignet sind. Damit werden erstmals inf-sup stabile Lagrange-Multiplikatorräume in der gemischt-dimensionalen Faser/Festkörper-Kopplung eingesetzt und die rechnerische Analyse ganzer faserverstärkter Komponenten und großer Systeme auf Supercomputern ermöglicht, ohne unter der schlechten Konditionierung und der fehlenden Diagonaldominanz von Penalty-Methoden zu leiden. |
| Kontakt am IMCS | Dr.-Ing. Matthias Mayr, Dr.-Ing. Ivo Steinbrecher, Dharini Balachandran M.Sc. |
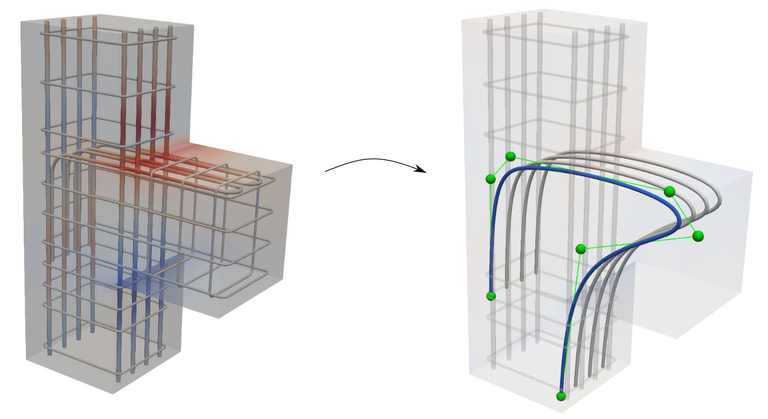
Individuelle Fließfertigung für Betonfertigteile
| Fördergeber | Bayerisches Verbundforschungsprogramm (BayVFP) |
| Laufzeit | 2023 - 2025 |
| Partner |
Institut und Labor für Konstruktiven Ingenieurbau, UniBw München |
| Kurzbeschreibung |
Im Rahmen des Verbundvorhabens Individuelle Fließfertigung für Betonfertigteile (IFB) wird eine durchgängig digitale Prozesskette zwischen Planung und Fertigung von Stahlbetonbauteilen geschaffen. Gleichzeitig werden modulare Fertigungslösungen unter Einsatz von Robotik und 3D-Druck entwickelt. Der Hauptbeitrag unseres Instituts besteht in der Optimierung von Bewehrungsgeometrien in nicht standardisierten Stahlbetonbauteilen. Herkömmliche Berechnungsverfahren resultieren bei solchen Bauteilen zu einer Überdimensionierung und damit zu einem nicht optimalen Einsatz von Ressourcen. Der am IMCS Entwickelte Ansatz baut auf modernsten gemischt-dimensionalen Kopplungsverfahren auf um den Verbund Stahlbeton möglichst detailgetreu und effizient zu simulieren. Dies erlaubt die Anwendung von Formoptimierungsalgorithmen für die Bewehrungsgeometrie. Die Forschungs- und Entwicklungsarbeiten erfolgen in enger Zusammenarbeit starker Partner aus der bayerischen Bauwirtschaft (Max Bögl), der additiven Fertigung (FIT AG) sowie der Forschung (Institut und Labor für Konstruktiven Ingenieurbau, UniBw München). |
| Kontakt am IMCS |
Steuerbare Metamaterialien und intelligente Strukturen
| Fördergeber | Deutsche Forschungsgemeinschaft (DFG) |
| Laufzeit | 2022 - 2026 |
| Partner | |
| Kurzbeschreibung |
Ziel dieses Projekts ist die Erforschung der Metamaterialeigenschaften von lokal periodischen Strukturen, die aus herkömmlichen und intelligenten Materialien bestehen. Die Steuerbarkeit durch elektroaktive Komponenten und geometrische Anordnungen, die sowohl zeitlich als auch räumlich variieren, bieten neuartige Merkmale, die sich von herkömmlichen passiven Metamaterialien unterscheiden. Neue Ansätze beruhen auf steuerbaren und anpassungsfähigen Strukturen, die mit eingebetteten Aktoren und Sensoren ausgestattet sind und ein höheres Maß an Multifunktionalität bieten, z. B. die Fähigkeit Schwingungen und Wellenausbreitung zu steuern, die Form zu verändern oder die Steifigkeit in Raum und Zeit zu modifizieren. Die Forschungsarbeiten sind in ein internationales Konsortium eingebettet und werden in enger Zusammenarbeit mit wissenschaftlichen Partnern an der Tschechischen Akademie der Wissenschaften in Prag (Tschechische Republik) und an der Westböhmische Universität in Pilsen (Tschechische Republik) durchgeführt. |
| Kontakt am IMCS |
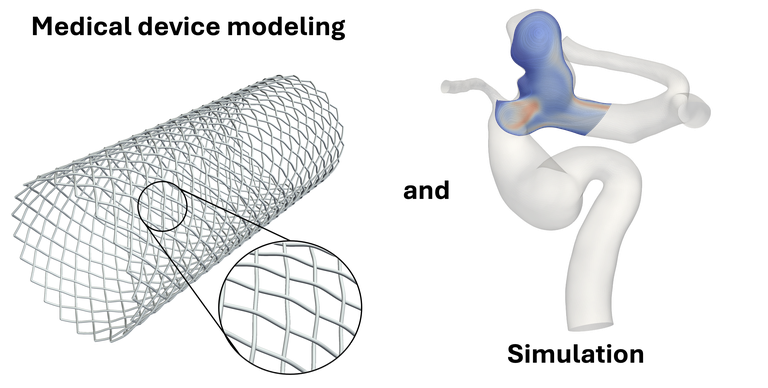
Mehrskalen-Algorithmen und Simulation für die patientenspezifische Optimierung von endovaskulären Eingriffen bei zerebralen Aneurysmen
| Fördergeber | DFG Schwerpunktprogramm 2311 |
| Laufzeit | 2021 - jetzt |
| Partner | Lehrstuhl für Numerische Mathematik, TU München Abteilung für Neuroradiologie, Klinikum rechts der Isar, TU München |
| Kurzbeschreibung |
In diesem Projekt, das in das DFG-Schwerpunktprogramm 2311 eingebettet ist, wird ein kontinuumsmechanischer Ansatz für die Simulation der endovaskulären Intervention in Hirnaneurysmen durch Coiling, Woven EndoBridges (Web) oder Flow Diverter entwickelt. Er zielt auf die patientenindividuelle Verbesserung der Behandlung von Hirnaneurysmen durch prädiktive Simulation und Optimierung.
Das IMCS ist aktiv an der numerischen Modellierung der verschiedenen Medizinprodukte und der beteiligten biochemischen Prozesse der Blutgerinnung im Aneurysma beteiligt. In Zusammenarbeit mit den Projektpartnern werden die Implantat- und Gerinnungsmodelle mit einem Lattice-Boltzman-basierten arteriellen Modell des Blutflusses gekoppelt, um das langfristige Behandlungsergebnis vorherzusagen und die Erfolgschancen zu quantifizieren.
|
| Kontakt am IMCS | Dr. Ing. Matthias Mayr, Martin Frank M.Sc. |
Mehrskalige Modellierung des thermomechanischen Reibkontakts von komplexen Problemen in technischen Anwendungen

| Fördergeber | Deutscher Akademischer Austauschdienst (DAAD) Ministero dell'Istruzione dell'Università e della Ricera (MIUR) |
| Laufzeit | 2018 - 2020, 2021 - 2025 |
| Partner | MUSAM Lab, IMT School for Advanced Studies Lucca, Italien (Prof. Paggi) |
| Kurzbeschreibung |
Ziel dieses Projekts ist die Entwicklung eines effizienten numerischen Zwei-Skalen-Schemas. Dabei sollen implizite Finite-Elemente-Berechnungen (FEM) auf der Makro-Skala und die Boundary-Elemente-Methode (BEM) auf der Mikro-Skala zum Einsatz kommen. Mit Hilfe dieses Ansatzes wird die genaue Lösung von Reibungs- und thermomechanischen Kontaktproblemen mit mikroskopischer Grenzflächenrauhigkeit berechnet. Das gesamte Spektrum der Reibungszustände, von der vollständigen Haftung über Zwischenzustände bis hin zum vollständigen Gleiten, wird ebenso behandelt wie jeder komplexe Belastungspfad. Das Zwei-Skalen-Modell wird mit einem vollständig aufgelösten 3D-FEM-Modell unter Verwendung von High-Performance-Computing (HPC)-Techniken verglichen. Reibungskontaktprobleme sind in vielen technischen und physikalischen Forschungsbereichen von Bedeutung. Im Maschinenbau treten sie bei Konfigurationen wie dem Rad-Schiene-Kontakt, Lagern, Bremsen oder Rad-Asphalt-Kontakt auf. Zu den Anwendungen des thermomechanischen Kontakts gehören Schraubverbindungen unter Temperaturbelastung und Schrumpfverbindungen. Reibung ist auch für die Wechselwirkung zwischen Boden und Pfahlgründung im Bauwesen und in der Geotechnik von Interesse, und in der Biomechanik führt die Relativbewegung in Hüftgelenksprothesen zu Abrieb. In all diesen Szenarien ist die Grenzfläche zwischen sich berührenden Körpern nicht mikroskopisch flach, sondern ihre Rauheit weist vielschichtige Merkmale auf, die die Verformung und die Spannungszustände im Material beeinflussen.
Das Projekt umfasst die Entwicklung einer BEM-Software auf Mikroebene namens MIRCO, ein Akronym für MUSAM-IMCS Rough Contact cOde. MIRCO wird aktiv weiterentwickelt und ist frei zugänglich. Es kann als konstitutives Kontaktgesetz in anderen FEM-Softwarepaketen verwendet werden, indem es als Bibliothek genutzt wird und steht auf GitHub zur Verfügung.
|
| Kontakt am IMCS | Dr.-Ing. Ivo Steinbrecher, Rishav Shaw M.Sc., Jacopo Bonari Ph.D. |
Effiziente numerische Algorithmen für die Lösung linearer Gleichungssysteme
| Fördergeber | Zentrum für Digitalisierungs- und Technologieforschung der Bundeswehr (dtec.bw) |
| Laufzeit | 2021 - 2026 |
| Partner | Institute im dtec.bw Project HPC.bw |
| Kurzbeschreibung | Effiziente numerische Algorithmen spielen in moderner Simulationssoftware eine entscheidende Rolle bei der Lösung von Problemen aus Biomechanik, Maschinenbau und dem Bauingenieurwesen. Speziell die Lösung von linearen Gleichungssystemen im Kontext von Multiphysikproblemen stellt eine Herausforderung dar, bei der skalierbare Vorkonditionierer eine kritische Rolle spielen. Innerhalb des Forschungsprojektes werden einerseits Ansätze zur Behandlung der problemspezifischen Blockstruktur der zu Grunde liegenden Matrix als auch neuartige algebraische Mehrgitteransätze entwickelt. Dies umfasst unter anderem die Neu- und Weiterentwicklung von Block- sowie Einzelfeldglättern, als auch neue Methoden zur Grobgitterkorrektur. Als Softwarumgebung dient das Multigrid-Framework MueLu und die Blockvorkonditinierer basierend auf Teko. Beide Softwarepakete sind in die Open-Source Bibliothek Trilinos eingebettet, um verteilte parallele Rechnungen auf modernster Hardware zu realisieren. Anwendung finden die entwickelten Verfahren einerseits in der parallelen Simulationen von Balken-Festkörper Problemen und heterogenen Materialien, wie sie zum Beispiel bei der Interaktion von Beton und Bewehrungsstahl auftreten. Andererseits werden die neuen Methoden für die Berechnung von Fluid-Festkörper Interaktionen aus der Biomechanik eingesetzt. |
| Kontakt am IMCS |
Hoch effiziente und parallel skalierbare Mortar-Methoden für Kontakt- und Mehrfeldprobleme
| Laufzeit | 2021 - 2024 |
| Partner | 4C-Projektpartner an der TU München und am Helmholtz Zentrum Hereon |
| Kurzbeschreibung |
Das Ziel des Promotionsprojektes ist die Weiterentwicklung der Kopplung physikalischer Mehrfeldprobleme mittels Mortar-Methoden mit besonderem Fokus auf die Anwendung im Bereich der nicht-linearen Kontaktmechanik. Aufgrund der intrinsisch nicht-linearen Natur der eingeführten Zwangsbedingungen an der Kontakoberfläche entstehen deutlich erhöhte Anforderungen unter anderem an Kontakt-Such-Algorithmen, nicht-lineare Löser, optimale Vorkonditionierung linearer Gleichungssysteme, eine vollständig konsistente Linearisierung des Problems für implizite Zeitintegration, sowie Mortar-spezifische Operationen wie z.B. die Berechnung der Netzverschneidung an der Kontaktfläche innerhalb jeder Newton-Iteration. Hochaufgelöste Simulatiosmodelle von Kontaktproblemen bestehen potentiell aus mehreren Millionen Freiheitsgraden, erfordern jedoch höhere Rechenleistung als vergleichbare Probleme aus der reinen Festkörpermechanik. Daher ist die Implementierung in einem parallelen Framework unumgänglich. Der erste Schritt des Promotionsprojekts ist die Entwicklung eines hoch parallel skalierbaren Frameworks in einer MPI-basierten "Distributed Memory Environment”, einer unabhängig verteilten Volumen- und Mortardiskretisierung, sowie eine optimale Lastverteilung auf den physikalischen Prozessorkernen. Die Implementierung erfolgt im Multiphysics Framework “4C” (in Kooperation mit der TU München und dem Helmholtz Zentrum Hereon). |
| Kontakt am IMCS | Dr.-Ing. Matthias Mayr, Christopher Steimer M.Sc. |
Nutzung der Eigenfrequenzen zur Identifikation von Rissen
| Laufzeit | 2021 - jetzt |
| Kurzbeschreibung | Im Mittelpunkt des Projekts steht die näherungsweise Berechnung von Eigenwerten verschiedener Differentialoperatoren auf Gebieten mit Rissen mithilfe isogeometrischer Analysis. Dabei sollen Methoden entwickelt werden, die es ermöglichen, dass die simulierten Eigenwerte möglichst genau die in der Praxis messbaren Eigenfrequenzen von Testobjekten mit Rissen darstellen und auch entsprechende Konvergenzergebnisse gezeigt werden. Anschließend sollen diese Eigenfrequenzen genutzt werden, um den Riss zu identifizieren, d.h., die Form des Risses zu bestimmen. Dieses inverse Problem soll mit einem neuronalen Netz gelöst werden, für dessen Training wir möglichst hochqualitative Simulationsdaten benötigen, um eine sinnvolle Anwendung in der Praxis garantieren zu können. |
| Kontakt am IMCS |
Kombination von Isogeometrischer Analyse, Finite-Elemente-Methoden und Embedded-Mesh-Kopplungsverfahren für Kontaktprobleme
| Fördergeber | Deutsche Forschungsgemeinschaft (DFG), eigene Finanzierung |
| Laufzeit | 2021 - jetzt |
| Kurzbeschreibung |
In den letzten Jahren wurden Kontaktformulierungen meist mit der klassischen Finite-Elemente-Methode (FEM) entwickelt. Ein typisches Finite-Elemente-Netz kann jedoch aufgrund der C0-Stetigkeit an Elementschnittpunkten kein kontinuierliches Normalenvektorfeld liefern. Eine gängige Lösung besteht darin, das Netz an der Kontaktoberfläche zu verfeinern, was üblicherweise zu einer unnötigen Ausdehnung der verfeinerten Elemente in das Domänenvolumen führt. Um eine Kontinuität höherer Ordnung an der Kontaktoberfläche zu erreichen, wurden in letzter Zeit Kontaktformulierungen unter Verwendung der Isogeometrischen Analyse (IGA) entwickelt. Diese verwenden typischerweise NURBS-Formfunktionen für die Geometriebeschreibung sowie die Approximation des Lösungsfeldes. Allerdings reichen die NURBS-Elemente wiederum in das Domänenvolumen hinein, wo ihre Kontinuität höherer Ordnung nicht unbedingt mehr Vorteile bietet (aufgrund der ohnehin reduzierten Regularität von Kontaktproblemen), sondern eher Rechenkosten verursacht. In diesem Projekt schlagen wir eine Trennung des Vernetzungsprozesses für die Kontaktoberfläche und für das innere Gebiet der beteiligten Körper vor, da die beiden Bereiche unterschiedliche Anforderungen an Kontinuität, Elementtyp, Netzorientierung und Netzverfeinerung stellen. Für die Diskretisierung der Kontaktoberfläche wird ein oberflächenorientiertes Randschichtnetz aus NURBS-Elementen erzeugt, welches lokal an gewünschten Stellen verfeinert werden kann, ohne die Netzauflösung im innern des Körpers zu beeinflussen. Der Volumenbereich wird dagegen mit klassischen finiten Elementen auf strukturierten kartesischen Gittern diskretisiert. Daraus ergeben sich zwei unabhängige, aber überlappende Netze, die über Embedded-Mesh-Kopplungsverfahren konsequent miteinander gekoppelt werden. Dazu werden geeignete Mortar-/Lagrange-Multiplikator-Methoden sowie die Nitsche-Methode untersucht.
|
| Kontakt am IMCS | Dr.-Ing. Ivo Steinbrecher, Eugenia Gabriela Loera Villeda M.Sc. |
Kombination von Daten- und Physik-basierten Methoden in hybriden digitalen Zwillinge
| Fördergeber | Zentrum für Digitalisierungs- und Technologieforschung der Bundeswehr (dtec.bw) |
| Laufzeit | 2021 - 2026 |
| Partner | Institute des dtec.bw Projekts RISK.twin im Rahmen des Forschungszentrums RISK |
| Kurzbeschreibung |
In diesem Projekt werden Methoden für hybride digitale Zwillinge von kritischen Infrastrukturen untersucht und weiterentwickelt. Der Schwerpunkt liegt dabei auf der Kombination von Physik-basierter Modellierung mit Finite-Elemente-Methoden (FEM) und datenbasierter Modellierung mit maschinellen Lernverfahren. Der erste Anwendungsfall sind Stahlbetonbrücken. Auf der Seite der physikalischen Modellierung wird ein gemischt-dimensionales FEM-Modell für Stahlbetonbauteile entwickelt. Ergänzend dazu werden Varianten von neuronalen Netzen untersucht. Beide werden kombiniert, um das Materialmodell mit Messdaten zu verbessern und um ein Modell reduzierter Ordnung für das physikalische Systems abzuleiten. Dabei wird auf die Allgemeinheit und Anwendungsunabhängigkeit der Methoden geachtet, sodass die entwickelten Techniken auch von den Projektpartnern genutzt werden können. Neue Algorithmen werden in Form einer eigenen Softwarelösung implementiert. Eine zugehörige Hardwareplattform für Hochleistungsrechnen wird im Data Science & Computing Lab bereitgestellt. |
| Kontakt am IMCS | Dr.-Ing. Daniel Wolff, Bishr Maradni M.Sc., Tarik Sahin M.Sc. |