Die aktuelle Forschung unseres Instituts auf dem Gebiet der Modellierung und Diskretisierung in der Mechanik konzentriert sich auf Fragestellungen der Kontakt- und Interfacemechanik, der gemischt-dimensionalen Modellierung, der gekoppelten Mehrfeldprobleme und der fortgeschrittenen Diskretisierungsverfahren.
Ansprechpartner am IMCS
Kontakt- und Interfacemechanik
Das IMCS ist international für seine innovative Forschung auf dem Gebiet der rechnergestützten Kontakt- und Interfacemechanik bekannt. Unsere Arbeiten umfassen das gesamte Spektrum von der mikromechanischen Modellierung (z.B. von rauen Oberflächen) und Tribologie (z.B. Elastohydrodynamik) bis hin zu robusten Diskretisierungsverfahren für große Verformungen (z.B. FEM, IGA) und effizienten Lösungsalgorithmen (z.B. semi-smooth Newton). Ein besonderer Schwerpunkt sind Mortar-Finite-Elemente-Methoden, wobei die Beiträge von den mathematischen Grundlagen bei Kontaktformulierungen (z.B. stabile Lagrange-Multiplikatorräume) bis hin zur praktischen Umsetzung und zum Hochleistungsrechnen (z. B. algebraische Mehrgitterverfahren) reichen. Nichtlineare Balken/Balken- und Balken/Festkörper-Kontaktformulierungen zur effizienten Modellierung von faserbasierten Systemen runden unser einzigartiges Kompetenzprofil ab. Die Gruppe betreibt hierbei sowohl Grundlagenforschung, insbesondere mit DFG-Förderung, als auch anwendungsorientierte Projekte, einschließlich erfolgreicher Industriekooperationen.
Schlüsselpublikationen
- Bonari, J., Marulli, M.R., Hagmeyer, N., Mayr, M., Popp, A., Paggi, M. (2020): A multi-scale FEM-BEM formulation for contact mechanics between rough surfaces, Computational Mechanics, 65(3):731-749, DOI
, arXiv 
- Popp, A., Wriggers, P. (Eds.) (2018): Contact Modeling for Solids and Particles, CISM International Centre for Mechanical Sciences 585, Springer International Publishing, Link
- Meier, C., Wall, W.A., Popp, A. (2017): A unified approach for beam-to-beam contact, Computer Methods in Applied Mechanics and Engineering, 315:972-1010, DOI
Aktuelle Projekte
Abgeschlossene Projekte
Gemischt-dimensionale Modellierung
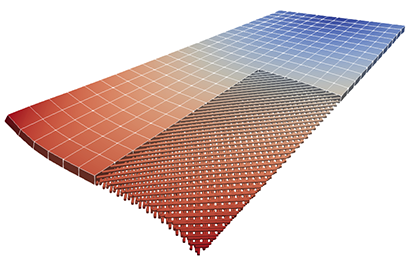Die Interaktion zwischen schlanken, faser- oder stabartigen Komponenten, bei denen eine räumliche Dimension deutlich größer ist als die beiden anderen, und 3D-Kontinua (z.B. Flüssigkeiten oder Festkörper) ist ein häufig anzutreffendes Phänomen in der realen Welt. Ein effizienter Ansatz zur Modellierung solcher Systeme besteht darin, nichtlineare 1D-Balkentheorien für die schlanken Strukturen zu verwenden, während etablierte numerische Modelle die 3D-Hintergrundkontinua behandeln. Dies erfordert einen gemischt-dimensionalen Kopplungsansatz, um die Wechselwirkungen zwischen den 1D-Fasern und den höher-dimensionalen Kontinua konsistent zu erfassen.Gemischt-dimensionale Probleme sind für ein breites Spektrum moderner technischer Anwendungen von entscheidender Bedeutung. Am IMCS entwickeln wir numerische Methoden und Modelle, um diese herausfordernden Aufgabenstellungen zu lösen - mit besonderem Schwerpunkt auf faserverstärkten Materialien in der Festkörpermechanik und der Fluid-Struktur-Interaktion. Darüber hinaus ist unsere Gruppe führend in der Entwicklung spezieller Lösungsverfahren, wie z.B. algebraischer Mehrgitterverfahren, und in der Implementierung leistungsfähiger Forschungssoftware, um diese komplexen Systeme effizient zu lösen.
Schlüsselpublikationen
- Hagmeyer, N., Mayr, M., Steinbrecher, I., Popp, A. (2022): One-way coupled fluid-beam interaction: Capturing the effect of embedded slender bodies on global fluid flow and vice versa, Advanced Modeling and Simulation in Engineering Sciences, 9:9, DOI (Open Access) , arXiv
- Steinbrecher, I., Popp, A., Meier, C. (2021): Consistent coupling of positions and rotations for embedding 1D Cosserat beams into 3D solid volumes. Computational Mechanics, DOI (Open Access)
- Steinbrecher, I., Mayr, M., Grill, M. J., Kremheller, J., Meier, C., Popp, A. (2020): A mortar-type finite element approach for embedding 1D beams into 3D solid volumes, Computational Mechanics, 66:1377-1398, DOI (Open Access)
Aktuelle Projekte
Abgeschlossene Projekte
Gekoppelte Mehrfeldprobleme
Die Wechselwirkung zwischen verschiedenen physikalischen Feldern ist ein zentraler Aspekt vieler technischer und biologischer Prozesse. Die Lösung solcher Probleme erfordert einen tiefen Einblick in das Zusammenspiel der beteiligten physikalischen Mechanismen und numerischen Methoden. Die Forschenden am IMCS befassen sich mit der Entwicklung von mathematischen Modellen, Berechnungsverfahren und skalierbaren Algorithmen im Zusammenhang mit gekoppelten Mehrfeld- und Grenzflächenproblemen, bei denen genau dieses Zusammenspiel zwischen Physik und Numerik die Robustheit und Effizienz der Berechnungen fördert.
Das IMCS verfügt über langjährige Expertise in Diskretisierungstechniken für Kopplungsoperatoren sowie in der Entwicklung effizienter und robuster Lösungsstrategien für gekoppelte Probleme. Prototypische Anwendungen sind oberflächengekoppelte Phänomene wie die Fluid/Struktur-Wechselwirkung oder gemischt-dimensionale Kopplungen wie die Faser/Festkörper- oder Faser/Fluid-Wechselwirkung.
Schlüsselpublikationen
- Hagmeyer, N., Mayr, M., Popp, A. (2024): A fully coupled regularized mortar-type finite element approach for embedding one-dimensional fibers into three-dimensional fluid flow, International Journal for Numerical Methods in Engineering, published online ahead of print, e7435, 2024, DOI (Open Access) , arXiv
- Seitz, A., Wall, W.A., Popp, A. (2018): A computational approach for thermo-elasto-plastic frictional contact based on a monolithic formulation employing non-smooth nonlinear complementarity functions, Advanced Modeling and Simulation in Engineering Sciences, 5:5, DOI (Open Access)
- Mayr, M., Klöppel, T., Wall, W.A., Gee, M.W. (2015): A temporal consistent monolithic approach to fluid-structure interaction enabling single field predictors, SIAM Journal on Scientific Computing, 37(1):B30-B59, DOI , arXiv
Aktuelle Projekte
Abgeschlossene Projekte
Fortgeschrittene Diskretisierungsverfahren
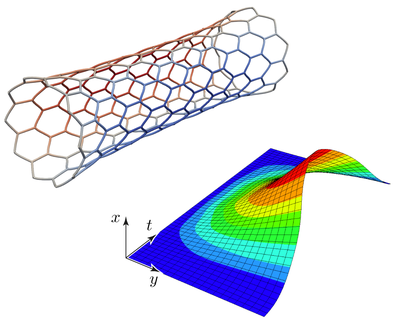Ein zentraler Aspekt unserer täglichen Arbeit in verschiedenen Forschungsbereichen und Projekten ist die Anwendung von 1D-Balkentheorien. Während etablierte numerische Methoden für viele Fälle ausreichend sind, profitieren bestimmte Anwendungen von fortgeschrittenen Balken Formulierungen, wie z.B. für schubsteife oder torsionsfreie Balkenmodelle, oder erfordern diese sogar. Am IMCS sind wir aktiv an der Entwicklung solcher Diskretisierungsverfahren beteiligt.
Ein weiterer aktueller Forschungsschwerpunkt am IMCS sind sogenannte Raum-Zeit-Finite-Elemente-Methoden, die einen einheitlichen Ansatz zur Diskretisierung der räumlichen und zeitlichen Dimensionen zur Lösung partieller Differentialgleichungen (PDEs) bieten. Diese Methoden sind besonders nützlich, da sie auf natürliche Weise Bewegungen, Verformungen und sogar veränderlichen Topologien im Berechnungsgebiet berücksichtigen. Im High-Performance-Computing (HPC) ermöglicht die Raum-Zeit-Diskretisierung "Parallel-in-Time (PinT)"-Berechnungen und erweitert die Parallelität über die räumlichen Dimensionen hinaus auch auf die Zeitachse.
Schlüsselpublikationen
- Meier, C., Popp, A., Wall, W. A. (2017): Geometrically exact finite eement formulations for slender beams: Kirchhoff–Love theory versus Simo–Reissner theory, Archives of Computational Methods in Engineering, 26,163–243, DOI
- Seitz, A., Farah, P., Kremheller, J., Wohlmuth, B. I., Wall, W. A., Popp, A. (2016): Isogeometric dual mortar methods for computational contact mechanics, Computer Methods in Applied Mechanics and Engineering, 301:259–280, DOI
- von Danwitz, M., Voulis, I., Hosters, N., Behr, M. (2023): Time‐continuous and time‐discontinuous space‐time finite elements for advection‐diffusion problems, International Journal for Numerical Methods in Engineering, 124:3117–3144, DOI