Overview
Optimal Control
Ordinary differential equations (ODEs) and differential-algebraic equations (DAEs) are widely used to model control systems in engineering, natural sciences, and economy. Optimal control plays a central role in optimizing such systems and to operate them efficiently and safely. Basically, an optimal control problem aims to minimize or maximize a given objective function subject to a dynamic system, constraints on controls or states, and boundary conditions. Typical applications are path planning tasks for UGVs, UAS, or robots, which often need to be performed in real-time.

Our research focuses on the following topics:
- derivation of necessary and sufficient optimality conditions for DAE optimal control problems
- convergence analysis for discretized optimal control problems
- direct discretization methods, specifically direct shooting methods and full discretization (collocation) methods
- dynamic programming techniques
- mixed-integer and hybrid optimal control
- bilevel optimal control problems, e.g. dynamic scheduling and Stackelberg games
- collision avoidance techniques
In addition, model design and simulation tools are part of our portfolio as well.
Optimization
Efficient optimization methods are at the core of every direct discretization method for optimal control problems, but of course optimization problems also occur in many other disciplines. Depending on the origin of the problem, the optimization problem can be convex or non-convex, small and dense, or large-scale and sparse. Solution methods need to be tailored to such structures in order to work efficiently. Linear-quadratic optimization problems deserve particular attention as they play an important role in linear model-predictive control and in iterative solution methods where they occur as subproblems.
Our group is active in algorithm development and in the analysis of certain classes of optimization problems:
- sequential quadratic programming (SQP) for small and dense and large-scale and sparse problems
- interior-point methods (IP) for linear-quadratic and nonlinear problems
- semi-smooth Newton methods for discretized optimal control problems
- generalized Nash equilibrium problems
- proximal augmented Lagrangian methods
- parametric sensitivity analysis and real-time optimization
Model-predictive Control (MPC)
Model-predictive control is a powerful and versatile optimization-based control concept, which is able to obey control and state constraints. The basic idea is to solve a (discretized) optimal control problem for the current state on a prediction horizon and to apply the first control of the control sequence to the system. Then, the prediction horizon is shiftet in time and the procedure is repeated. This way, MPC constitutes a feedback control law. The computational bottleneck is typically the underlying optimizer, which needs to be fast and robust.
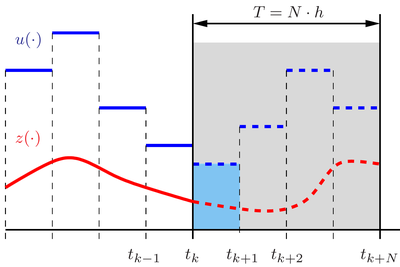
We use MPC extensively for path following and path planning tasks and investigate the following aspects:
- multi-step model-predictive control
- use of parametric optimization in model-predictive control
- imitation learning model-predictive control
- design of path following controllers using model-predictive control
- economic model-predictive control as a tool for path planning
- tailored QP and NLP methods and software packages for model-predictive control
Dynamic Inversion Control
Dynamic inversion is a control concept which is well suited for path following problems. We often use it in combination with model-predictive control as a low-level controller, which tracks the mpc-generated trajectories. Since dynamic inversion usually does not involve costly operations, it can work at a high frequency. The underlying idea is to invert the dynamics of a system in order to find the control input which corresponds to a given reference path. Then, feedback terms are added such that the error dynamics in case of deviations from the reference path become asympotically stable.
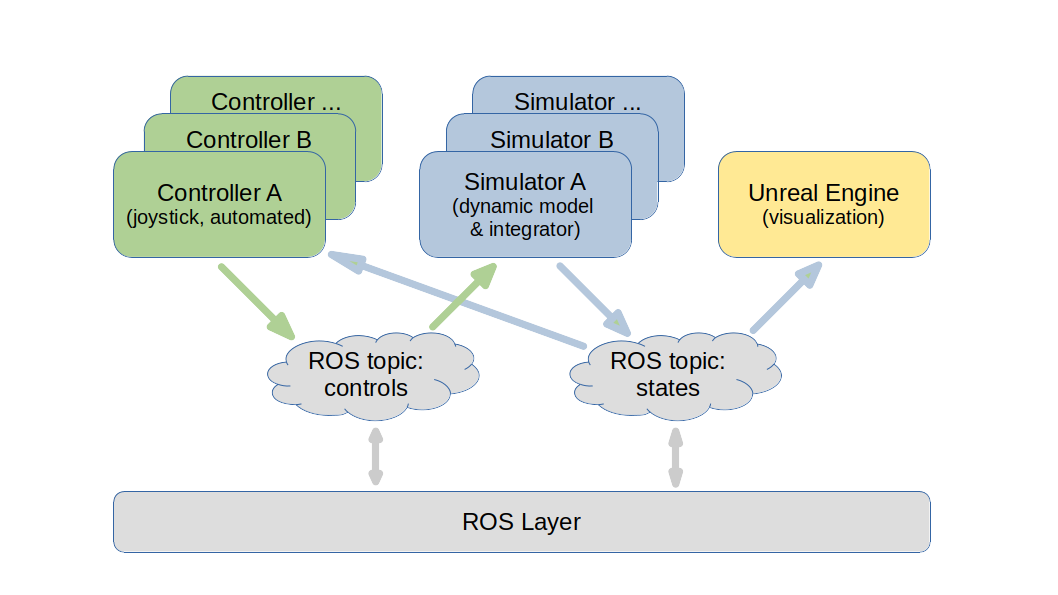
Automatic Control Architecture
The robot operating system ROS is used as a tool to realistically simulate and eventually deploy control procedures. Herein, ROS provides the communication layer and coordinates the exchange of data between the system (simulated or real) and the controller (e.g. a model-predictive controller). The interface to the Unreal Engine essentially takes the current state and visualizes the system accordingly. This concept is simple but effective. It is flexible and well-suited for multi-agent systems.
Software
The following software packages have been implemented in C++ or Fortran 90. They have been valuable tools to solve problems from various applications.
Optimal Control and Parameter Identification Problems
OCPID-DAE1
The software package OCPID-DAE1 is designed to solve optimal control problems and parameter identification problems subject to ordinary differential equations and differential algebraic equations, control and state constraints, and boundary conditions. It implements a direct multiple shooting method and uses the sqpfiltertoolbox to solve the discretized optimal control problems. It is written in Fortran 90. It can handle implicit differential equations (DAEs) and piecewise defined dynamics. It offers an adjoint estimation and allows to perform a parametric sensitivity analysis.
OCPPIDlight
OCPIDlight is a lean version of OCPPID-DAE1 with less options. It is available in C++ and Fortran 90.
nsn4ocp
The software package nsn4ocp implements a semi-smooth Newton method for nonlinear optimal control problems in C++. It uses a full discretization method and exploits the sparsity of the resulting discretized optimal control problem.
nsn4lqocp
The software package nsn4lqocp implements a semi-smooth Newton method for linear-quadratic optimal control problems in C++. It uses a full discretization method and exploits the sparsity of the resulting discretized optimal control problem. It is well-suited for linear model-predictive control applications.
OCPBasic
The code OCPBasic was developped by Dr. Andreas Huber and is available under this link. It is written in C++ and implements a full discretization method for nonlinear optimal control problems using the interior-point method IPBasic for the solution of the discretized problems.
Nonlinear Optimization Problems (NLPs)
sqpfiltertoolbox
The sqpfiltertoolbox implements different sequential-quadratic and sequential-linear programming methods for general nonlinear optimization problems in Fortran 90. The user can choose from different line-search strategies with merit functions or filter techniques to achieve convergence from arbitrary starting points. Derivatives can be provided by the user or are approximated automatically by finite difference approximations. In addition, a parametric sensitivity analysis can be performed. The code is designed for small-scale to medium-scale dense problems.
sqpfiltertoolbox (sparse)
This is the sparse version of the sqpfiltertoolbox, which is designed for large-scale and sparse problems. It is still under development and written in Fortran 90.
sqptoolbox
The sqptoolbox is the C++ version of the sqpfiltertoolbox without filter methods. The user can choose from different line-search strategies with merit functions to achieve convergence from arbitrary starting points. Derivatives can be provided by the user or are approximated automatically by finite difference approximations. The code is designed for small-scale to medium-scale dense problems.
WORHP
WORHP is a software package for large-scale and sparse nonlinear optimization problems. It was initially developed by the working groups of Prof. Christof Büskens (University of Bremen) and Prof. Matthias Gerdts (University of the Bundeswehr Munich) with funding from ESA and DLR. It is available under this link.
Quadratic Programming Problems (QPs)
Several QP solvers for dense or sparse linear-quadratic optimization problems have been developed at the Engineering Mathematics Group. They are mainly used within SQP methods and for linear model-predictive control tasks. The following implementations are available:
- QPDO by Dr. Alberto De Marchi is designed for general convex QPs and is available at this link. It is a primal-dual Newton proximal method.
- Semi-smooth Newton method for sparse, large-scale, and strictly convex linear-quadratic problems (in Fortran 90)
- Semi-smooth Newton method for small and dense linear-quadratic problems (in C++)
- Primal-dual interior-point method for large-scale and sparse strictly convex linear-quadratic problems (in Fortran 90)
- Primal active set methods for small and dense and large-scale and sparse strictly convex linear-quadratic problems (in Fortran 90)
- Primal active-set method for small and dense strictly convex linear-quadratic problems (in C++)
ROCS - Real-time Optimization and Control Simulator

The Realtime Optimization and Control Simulator (ROCS) is a software package written in Qt3D with Unreal Engine frontend. It is being developped under the lead of Dr. Andreas Britzelmeier at the Engineering Mathematics Group of the Universität der Bundeswehr München. It is a versatile tool to visualize and control vehicles, aircrafts, and robots in complex scenarios.
Books
The books contain the fundamental theory and selected algorithms in optimal control and optimization.
Optimal Control of ODEs and DAEs
|
Matthias Gerdts: 2nd Edition |
Abstract:
Mathematische Optimierungsverfahren des Operations Research
|
Matthias Gerdts, Frank Lempio |
Abstract:
Das Operations Research beschäftigt sich mit der Modellierung, qualitativen und quantitativen Analyse und algorithmischen Lösung von Entscheidungsproblemen. Es stellt Instrumente zur Analyse und Optimierung vernetzter Systeme bereit - u.a. in Wirtschaftsunternehmen, in der Städte- und Verkehrsplanung, Volkswirtschaft und Technik.
Es ist gleichermaßen Anwendungsfeld und Motivationsquelle für die in dieser Publikation behandelten Optimierungsverfahren. Deren Konzepte, theoretische Grundlagen und Eigenschaften werden ausführlich dargestellt. Zahlreiche Illustrationen unterstützen die Anschauung, viele vollständig durchgerechnete Beispiele tragen zum Verständnis bei und helfen beim Lösen der Übungsaufgaben.
Das Buch richtet sich an Studierende mathematischer Studiengänge, aber auch an mathematisch interessierte Studierende ingenieur- und wirtschaftswissenschaftlicher Studiengänge sowie an Wissenschaftler aus den Bereichen Mathematik, Wirtschaftsmathematik, Technomathematik, Wirtschafts- und Ingenieurwissenschaften, die an einer Einführung in Theorie und Verfahren der Optimierung interessiert sind.
- Klare und ausführliche Darstellung der mathematischen Optimierung
- Zahlreiche Beispiele, Übungsaufgaben und Testprogramme (auch online verfügbar)
- Gleichermaßen für Studierende und Praktiker geeignet


