Partikeldämpfung mit additiver Fertigung

Motivation

In den letzten Jahren hat der Einsatz der additiven Fertigung (AM) in industriellen Strukturanwendungen an Bedeutung gewonnen, da AM und insbesondere der Laser Powder Bed Fusion Prozess (PBF-LB) im Vergleich zu konventionellen Fertigungsverfahren mehrere Vorteile bietet [1]. Relevant für das hier präsentierte Forschungsprojekt sind die Fähigkeiten zur Herstellung einerseits von integralen Bauteilen und andererseits von Leichtbaustrukturen. Integrale Bauteile sind so konzipiert, dass sie aus möglichst wenigen Teilen bestehen, wobei jedes Teil mehrere Funktionen übernimmt [2]. Dies ist nicht nur aus Sicht einer industriellen Fertigung von Vorteil, sondern auch aus Sicht der Performanz des Bauteils, da es die Festigkeit erhöht und das Gewicht verringert. Dies ist insbesondere in der Luft- und Raumfahrt, der Automobilindustrie und im Energiesektor von Vorteil [3]. Ein oft gewünschtes hohes Steifigkeits-Gewichts-Verhältnis kann durch Topologieoptimierung erreicht werden und dessen geometrisch komplexe Lösungen sind besonders für die Herstellung durch PBF-LB geeignet [4]. Mehrere industrielle Anwendungen zeigen bereits, dass PBF-LB zur Herstellung leichter, vergleichsweise steifer und integral gestalteter Strukturbauteile eingesetzt wird [5]. Doch diese spezifischen Vorteile werden zu Nachteilen, wenn die Bauteile unter Vibration stehen, da leichte Strukturen anfälliger für Schwingungen sind [6], steife Strukturen eine geringere Bauteildämpfung aufweisen und die fehlende Reibung in Verbindungselementen die Dämpfungseigenschaften von integral konstruierten Bauteilen vermindert [7]. Dies führt zu einer geringeren Lebensdauer der Bauteile und zu einer höheren Schallabstrahlung.

Eine Methode diesen Anfälligkeiten entgegenzuwirken, ist der Einsatz von Partikeldämpfung. Bei diesem passiven Dämpfungssystem besteht das Bauteil aus einer festen (primären) Masse und einer beweglichen (sekundären) Partikelmasse. Diese Sekundärmasse kann als Außenbehälter an der Primärmasse befestigt oder in die Primärmasse eingefügt werden [8]. Unter Vibration gibt die Sekundärmasse durch inelastische Stöße oder Reibung zwischen den Partikeln oder zwischen Partikel und Wand Energie ab, siehe Abb. 1 [9].

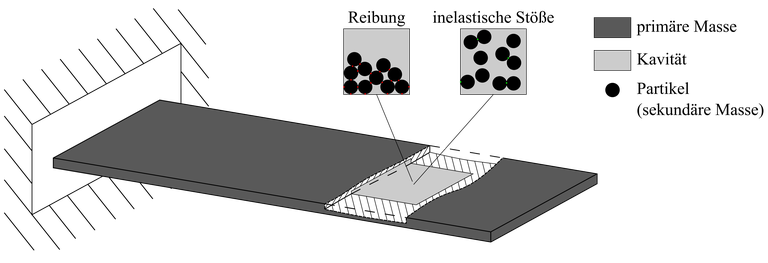
Schematische Darstellung eines additiv gefertigten Partikeldämpfers mit den beiden Wirkungsmechanismen der Energiedissipation; basierend auf [13] (aus [14])

PBF-LB bietet die Möglichkeit, die Partikeldämpfung inhärent in die Konstruktion eines Bauteils einzubeziehen, indem Hohlräume im Inneren des Bauteils entworfen werden, in denen nach der Herstellung ungeschmolzenes Pulver verbleibt. In Anlehnung an das Konzept "Complexity for free" [10] haben Ehlers et al. [11] den Begriff "Damping for free" geprägt, da diese Technik weder die Bauteilmasse noch die Herstellungskosten im Vergleich zu einem vollständig geschmolzenen Referenzbauteil erhöht. Allerdings ist die Modellierung von konventionellen und AM-Partikeldämpfern bisher nicht zuverlässig, da die Dämpfungseigenschaften in hohem Maße nichtlinear sind und von mehreren Konstruktionsparametern wie der Kavitätsgröße, der Kavitätsposition, der Anregungsamplitude und -frequenz abhängen [12]. Um diese Anwendung der additiven Fertigung besser zu verstehen, wurden im Rahmen dieses Teilprojektes Proben mit Partikeldämpfung aus der Aluminium-Legierung AlSi10Mg mittels PBF-LB hergestellt und auf deren Dämpfungseigenschaften getestet. Der beispielhafte, zukünftige Anwendungsfall einer Turbinenschaufel wurde durch die Wahl einer dünnen und flachen Kavität in Betracht gezogen.

Vorgehensweise

Es wurden zwei Arten von Probekörpern entworfen. Die zwei "massiven" Proben sind vollständig verschmolzen und dienen als Basis für die Modalparameter. Die drei "Kavitäts"-Proben haben die gleiche äußere Geometrie wie die massiven Proben und unterscheiden sich nur durch einen inneren Hohlraum, dessen Position so gewählt wurde, dass er nicht mit einem Knotenpunkt in den ersten drei Biegemoden überlappt. Allerdings fallen ein Knotenpunkt der vierten Biegemode und der Hohlraum überein. Die Dimensionen der Probekörper und die ersten vier Biegemoden können in Abb. 2 gesehen werden.

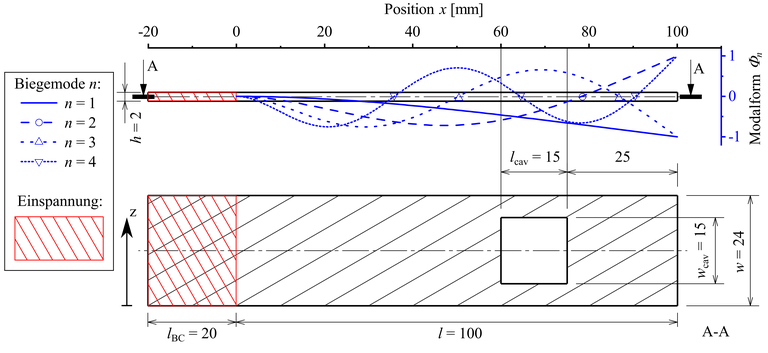
Abmessungen der „Kavitäts"-Proben in mm mit dem eingespannten Bereich (rot) und der Druckrichtung (z) sowie die Biege Modalformen Φ_n(x) für n = 1...4 mit den jeweiligen Knotenpunkten nach der klassischen Balkentheorie [14]

Die Proben werden nacheinander in einen elektrodynamischen Schwingerreger eingespannt, um ihre Modalparameter zu analysieren. Die Systemanregung wird mit einem Beschleunigungsaufnehmer an der Einspannung und die Systemantwort mittels abtastender Laser-Doppler-Vibrometrie (SLDV) gemessen, siehe Abb. 3. Die Anregungsbeschleunigung wird über alle Frequenzen innerhalb einer Messung konstant gehalten, um eine bessere Vergleichbarkeit zwischen den Moden zu ermöglichen. Nach einer Messreihe wird sie dann von 100 mm/s2, 200 mm/s2, 400 mm/s2 bis auf 800 mm/s2 pro Frequenzbereich erhöht, um die bereits erwähnten nichtlinearen Dämpfungseigenschaften der Partikeldämpfung zu ermitteln. Die Verteilung der Partikel in der Kavität vor und nach der Modalanalyse wird mit Hilfe von Computertomographie (CT) untersucht.

Versuchsaufbau des elektrodynamischen Schwingerregers mit einer Probe in der Einspannung, dem Beschleunigungsmesser zur Messung der Systemanregung und dem Laserpunkt des SLDV zur Messung der Systemantwort [14]

Resultate

Mit diesem experimentellen Aufbau werden die ersten vier Biegemoden und die ersten zwei Torsionsmoden angeregt. Die entsprechenden Modenformen sind in Abb. 4 zu sehen.

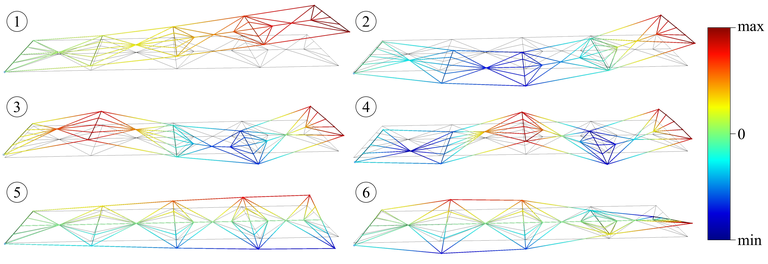
Qualitativer Vergleich zwischen den Verschiebungen der ersten sechs Schwingungsformen; (1) - (4) zeigen die ersten vier Biegemoden und (5) & (6) zeigen die ersten beiden Torsionsmoden [14]

Die Daten der ersten Biegemode werden nicht berücksichtigt, da große Auslenkungen zu parasitärer Reibung in der Einspannung führt, die die Bauteildämpfung beeinflusst [13]. Der Vergleich der Dämpfung als Verlustfaktoren  aller Proben für alle betrachteten Biegemoden ist in Abb. 5 zu sehen. Die Biegemoden zeigen für die kleineren Anregungsamplituden wenig bis keine Dämpfungswirkung. Bei höheren Anregungsamplituden nimmt die Dämpfungswirkung allerdings stark zu. Ein positiver Dämpfungseffekt ist für alle Biegemoden zu erkennen, am deutlichsten jedoch für die dritte Biegemode. Die Dämpfung der Torsionsmoden wurde ebenfalls analysiert, aber es wurde kein signifikanter Dämpfungseffekt gemessen.

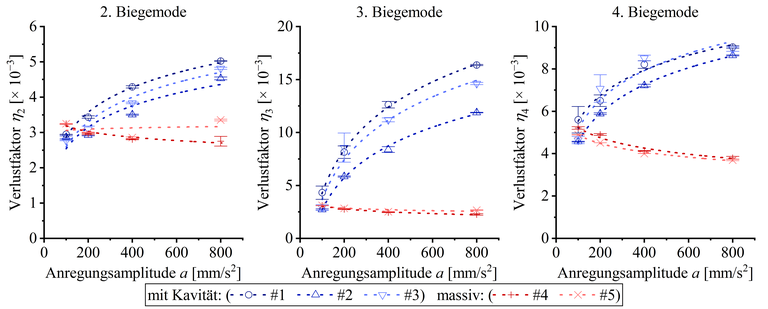
Verlustfaktor  aller Proben für die zweite bis vierte Biegemode n = 2...4 über der Anregungsamplitude a; die Daten folgen logarithmischen Trendkurven [14]

Ausblick

Die Abhängigkeit des Dämpfungseffekts von der Mode, der Anregungsamplitude sowie des spezifischen Probekörpers muss in zukünftigen Studien noch genauer untersucht werden. Zusätzlich hat sich während der Versuche ein Setzen des Pulvers in der Kavität gezeigt, welches zu einer Verringerung der Dämpfung über die Zeit führte. Dieser Effekt muss genau wie die Auswirkungen der additiven Fertigung auf die Streuung des Dämpfungseffektes noch untersucht werden um ein analytischen Modells zur Berechnung des Dämpfungseffektes zu erstellen.

Literatur 

1. Liu G, Zhang X, Chen X et al. (2021) Additive manufacturing of structural materials. Mater Sci Eng.: R: Rep 145:1–67. https://doi.org/10.1016/j.mser.2020.100596
2. May D (2021) Integrated Product Development with Fiber-Reinforced Polymers, 1st edn. Engineering Materials. Springer International Publishing, Cham
3. Degischer H-P, Lüftl S (2009) Leichtbau: Prinzipien, Werkstoffauswahl und Fertigungsvarianten, 1st edn. Wiley-VCH, Weinheim
4. Suresh S (2020) Topology Optimization for Additive Manufacturing Involving High-Cycle Fatigue. Licentiate Thesis, Linköping University
5. Anusci V (2018) Airbus Helicopters to begin 3D printing metal A350 components. https://www.3dprintingmedia.network/airbus-helicopters-a350/. Accessed 09 Nov 2021
6. Vajna S, Gerhard D, Wartzack S et al. (2018) CAx für Ingenieure: Eine praxisbezogene Einführung, 3rd edn. Springer Vieweg Berlin, Heidelberg
7. Dinkler D (2017) Einführung in die Strukturdynamik: Modelle und Anwendungen, 2nd edn. Springer Vieweg, Wiesbaden
8. Marhadi KS, Kinra VK (2005) Particle impact damping: effect of mass ratio, material, and shape. J Sound Vib 283:433–448. https://doi.org/10.1016/j.jsv.2004.04.013
9. Friend RD, Kinra VK (2000) Particle impact damping. J Sound Vib 233:93–118. https://doi.org/10.1006/jsvi.1999.2795
10. Hopkinson N, Hague R, Dickens PM (2005) Rapid Manufacturing: An Industrial Revolution for the Digital Age. John Wiley & Sons, Ltd, Chichester, UK
11. Ehlers T, Tatzko S, Wallaschek J et al. (2021) Design of particle dampers for additive manufacturing. Addit Manuf 38:1–19. https://doi.org/10.1016/j.addma.2020.101752
12. Fowler BL, Flint EM, Olson SE (2001) Design methodology for particle damping. In: Inman DJ (ed) Smart Structures and Materials 2001: Damping and Isolation, 1st edn. SPIE, pp 186–197
13. Ehlers T, Lachmayer R (2022) Design of Particle Dampers for Laser Powder Bed Fusion. Appl Sci 12:2237. https://doi.org/10.3390/app12042237
14. Westbeld J, von Coburg F, Höfer P (2023) Forced-response characterization of PBF-LB/AlSi10Mg particle dampers with thin and flat cavities. https://doi.org/10.1007/s40964-023-00428-5